
A function is a rule which indicates an operation to perform. e.g:
if f(x) = x² + 3
f(2) = 2² + 3 = 7 (i.e. replace x with 2)
Functions can be graphed. For example, the graph of f(x) = 1/x is as follows:
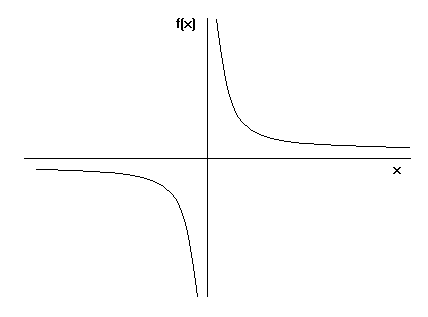
This is the same graph as y = 1/x, although the y axis is f(x) instead of y.
Types of graphs
The graph of y = k/x (f(x) = k/x) is known as a hyperbola. Asymptotes are lines on a graph which the graph gets very close to, but never touches. Therefore in the case of y = 1/x, the x and y axes are asymptotes.
Parabolas are graphs of y = ax² + bx + c . They can be 'U' shaped, when a is greater than zero, or 'n' shaped, when a is less than zero.
Graph Shifting
If you add 1 to f(x), this will shift the graph up 1 unit. i.e. f(x) + n shifts the graph upwards by n units.
f(x - 1) will shift the graph 1 unit to the right. i.e. f(x - n) shifts the graph n units to the right.
f(x + n) will shift the graph n units to the left.
Inverse Functions
The inverse function of y = 2x is y = ½x . The inverse of a funtion does the opposite of the function. To find the inverse of a function, follow the following procedures: let y = f(x). Swap all y's and x's . Rearrange to give y = . This is the inverse function.
Example:
f(x) = 3x - 7
y = 3x - 7 (let f(x) = y)
x = 3y - 7 (swap x's and y's)
y = x + 7
3
Combining Functions
If f(x) = 3x + 1 and g(x) = x² + 2
therefore f(x) + g(x) = 7
so 3x + 1 + x² + 2 = 7
so (x - 1)(x + 4) = 0
so x = 1 or -4